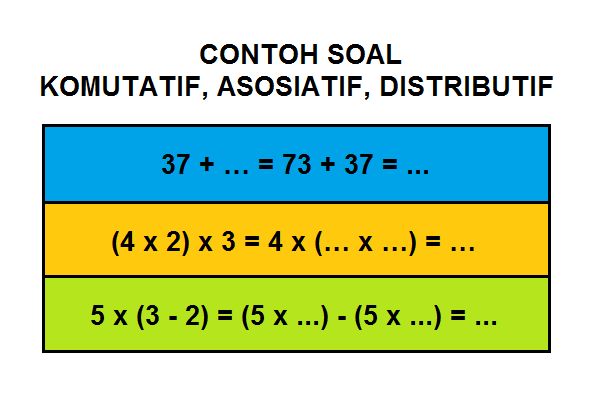
Pemahaman tentang sifat distributif dalam matematika adalah salah satu fondasi penting yang membantu siswa dan pelajar memahami bagaimana operasi aljabar bekerja. Sifat distributif sering muncul dalam berbagai bentuk, baik dalam penjumlahan maupun perkalian, dan merupakan salah satu dari tiga sifat dasar dalam aritmetika, bersama dengan sifat komutatif dan asosiatif. Meskipun terdengar rumit, sebenarnya sifat ini cukup sederhana dan mudah dipahami jika dilihat dari sudut pandang yang tepat.
Dalam konteks matematika, sifat distributif menggambarkan cara kita mengalikan bilangan dengan jumlah atau selisih. Misalnya, ketika kita mengalikan sebuah angka dengan jumlah dua bilangan lain, hasilnya sama dengan jumlah hasil perkalian angka tersebut dengan masing-masing bilangan. Hal ini sangat berguna dalam menyederhanakan ekspresi matematika yang kompleks dan membantu dalam proses perhitungan yang lebih efisien.
Artikel ini akan membahas secara rinci mengenai apa itu sifat distributif, bagaimana cara kerjanya, serta contoh penerapannya dalam kehidupan sehari-hari. Kami juga akan menjelaskan bagaimana sifat ini digunakan dalam aljabar dan bagian-bagian lain dari matematika. Dengan informasi yang lengkap dan jelas, pembaca diharapkan dapat memahami konsep ini dengan lebih baik dan menerapkannya dalam berbagai situasi.
Apa Itu Sifat Distributif?
Sifat distributif adalah salah satu dari tiga sifat dasar dalam matematika yang digunakan untuk menggambarkan hubungan antara operasi penjumlahan dan perkalian. Secara umum, sifat ini menyatakan bahwa pengalian suatu bilangan dengan jumlah dua bilangan lain akan menghasilkan hasil yang sama dengan jumlah hasil perkalian bilangan tersebut dengan masing-masing bilangan.
Secara matematis, sifat distributif dapat ditulis sebagai berikut:
a × (b + c) = (a × b) + (a × c)
Di mana:
– a, b, dan c adalah bilangan real.
– × menunjukkan operasi perkalian.
– + menunjukkan operasi penjumlahan.
Contohnya, jika a = 2, b = 3, dan c = 4, maka:
– 2 × (3 + 4) = 2 × 7 = 14
– (2 × 3) + (2 × 4) = 6 + 8 = 14
Hasilnya sama, sehingga sifat distributif terpenuhi.
Sifat ini juga berlaku untuk pengurangan:
a × (b – c) = (a × b) – (a × c)
Contoh:
– 5 × (6 – 2) = 5 × 4 = 20
– (5 × 6) – (5 × 2) = 30 – 10 = 20
Sifat distributif sangat penting karena memungkinkan kita untuk menyederhanakan ekspresi matematika yang rumit. Dengan memahami sifat ini, kita bisa mengubah bentuk persamaan agar lebih mudah diselesaikan atau dianalisis.
Sejarah dan Perkembangan Sifat Distributif
Konsep sifat distributif sudah dikenal sejak zaman kuno, meskipun istilah “sifat distributif” sendiri baru muncul dalam matematika modern. Para ahli matematika seperti Euclid dan Al-Khwarizmi telah menggunakan prinsip-prinsip serupa dalam karya-karyanya, meskipun tidak secara eksplisit menyebutnya sebagai sifat distributif.
Dalam abad ke-19, matematikawan seperti George Boole dan Augustus De Morgan mulai mengembangkan aljabar abstrak, yang kemudian menjadi dasar bagi pemahaman modern tentang sifat-sifat aljabar seperti distributif. Mereka menunjukkan bahwa sifat ini tidak hanya berlaku pada bilangan nyata, tetapi juga pada struktur aljabar yang lebih kompleks, seperti vektor dan matriks.
Perkembangan ini sangat penting karena memungkinkan matematika untuk berkembang menjadi ilmu yang lebih universal dan aplikatif. Sifat distributif kini digunakan dalam berbagai bidang, termasuk ilmu komputer, fisika, dan ekonomi.
Contoh Penerapan Sifat Distributif
Sifat distributif memiliki banyak penerapan dalam kehidupan sehari-hari dan berbagai bidang studi. Berikut beberapa contoh penerapan sifat distributif:
- Penyederhanaan Ekspresi Aljabar
Misalnya, kita ingin menyederhanakan ekspresi berikut:
3(x + 5) = 3x + 15
Dengan menggunakan sifat distributif, kita mengalikan 3 dengan x dan 5, lalu menjumlahkan hasilnya.
- Perhitungan Aritmetika
Jika kita ingin menghitung 7 × 12, kita bisa memecah 12 menjadi 10 + 2:
7 × (10 + 2) = (7 × 10) + (7 × 2) = 70 + 14 = 84
Ini memudahkan perhitungan tanpa perlu mengalikan langsung 7 × 12.
-
Penggunaan dalam Program Komputer
Dalam pemrograman, sifat distributif digunakan untuk mengoptimalkan kode. Misalnya, jika kita memiliki ekspresi sepertia * (b + c), kompiler mungkin akan mengubahnya menjadi(a * b) + (a * c)agar lebih efisien dalam eksekusi. -
Analisis Data dan Statistik
Dalam analisis data, sifat distributif digunakan untuk memecah data menjadi bagian-bagian yang lebih kecil, sehingga memudahkan perhitungan rata-rata, deviasi standar, dan lainnya. -
Ekonomi dan Keuangan
Dalam ekonomi, sifat distributif digunakan untuk menghitung biaya produksi, pendapatan, dan profit. Misalnya, jika perusahaan memiliki biaya tetap dan biaya variabel, mereka bisa menggunakan sifat distributif untuk menghitung total biaya.
Manfaat Memahami Sifat Distributif
Memahami sifat distributif memberikan banyak manfaat, terutama bagi siswa dan pelajar matematika. Beberapa manfaat utamanya meliputi:
-
Meningkatkan Kemampuan Berpikir Logis
Sifat distributif melatih otak untuk berpikir secara logis dan sistematis, yang sangat penting dalam menyelesaikan masalah matematika. -
Mempermudah Penyelesaian Persamaan
Dengan memahami sifat ini, siswa bisa menyederhanakan persamaan dan menyelesaikannya dengan lebih cepat dan akurat. -
Membuka Wawasan dalam Aljabar
Sifat distributif adalah dasar dari aljabar, sehingga memahaminya akan memperkuat pemahaman siswa terhadap konsep-konsep aljabar yang lebih kompleks. -
Meningkatkan Keterampilan Matematika Umum
Sifat distributif digunakan dalam berbagai situasi matematika, baik dalam bentuk penjumlahan, pengurangan, maupun perkalian, sehingga meningkatkan keterampilan matematika secara keseluruhan. -
Mendorong Kreativitas dalam Solusi Masalah
Dengan memahami sifat distributif, siswa bisa mencoba berbagai pendekatan untuk menyelesaikan masalah, yang memacu kreativitas dan inovasi.
Kesimpulan
Sifat distributif adalah salah satu konsep matematika yang sangat penting dan sering digunakan dalam berbagai bidang. Dengan memahami sifat ini, siswa dan pelajar bisa meningkatkan kemampuan berpikir logis, mempermudah penyelesaian persamaan, serta memperkuat dasar aljabar. Selain itu, sifat ini juga memiliki banyak penerapan dalam kehidupan sehari-hari dan berbagai bidang studi seperti ekonomi, ilmu komputer, dan statistik.
Jika Anda ingin mempelajari lebih lanjut tentang sifat distributif atau ingin memahami konsep-konsep matematika lainnya, disarankan untuk terus belajar dan mencari referensi yang akurat dan terpercaya. Dengan pengetahuan yang cukup, Anda akan mampu menghadapi berbagai tantangan matematika dengan lebih percaya diri.













Komentar