Pengertian dan Jenis Sudut dalam Geometri yang Wajib Diketahui

Sudut adalah salah satu konsep dasar dalam matematika, khususnya dalam bidang geometri. Sudut muncul ketika dua garis atau sinar berpotongan di satu titik, yang disebut sebagai titik sudut. Pemahaman tentang sudut sangat penting karena digunakan dalam berbagai bidang seperti arsitektur, teknik, fisika, dan bahkan dalam kehidupan sehari-hari. Misalnya, dalam olahraga sepak bola, pemain memperhatikan sudut tendangan agar dapat menciptakan peluang gol yang optimal. Di sisi lain, dalam desain bangunan, sudut menjadi elemen kunci dalam membentuk struktur yang kokoh dan estetis.

Dalam matematika, sudut dinyatakan dengan simbol ∠ dan diukur dalam satuan derajat (°). Rentang ukuran sudut berkisar dari 0° hingga 360°. Setiap sudut memiliki karakteristik unik berdasarkan besarnya, sehingga memungkinkan pengelompokan menjadi beberapa jenis. Memahami berbagai jenis sudut tidak hanya membantu dalam menyelesaikan soal-soal matematika, tetapi juga meningkatkan kemampuan kita untuk mengamati dan memahami bentuk-bentuk di sekitar kita.

Iklan Google Ads

Jasa Penerbitan Buku ISBN

Penerbitan buku ISBN dengan Layanan Cepat, Harga Murah dan Kerjakan Oleh Tim Profesional

jasapenerbitanbuku.com

Pengelompokan sudut berdasarkan besarannya mencakup sudut lancip, siku-siku, tumpul, lurus, refleks, penuh, dan nol derajat. Selain itu, sudut juga bisa dikategorikan berdasarkan hubungan antara dua sudut, seperti sudut berpenyiku, berpelurus, berdampingan, dan bertolak belakang. Pengetahuan ini akan sangat bermanfaat bagi siswa, guru, maupun siapa pun yang tertarik pada ilmu matematika. Berikut penjelasan lengkap mengenai pengertian dan jenis-jenis sudut dalam geometri.

Pengertian Dasar Sudut dalam Matematika

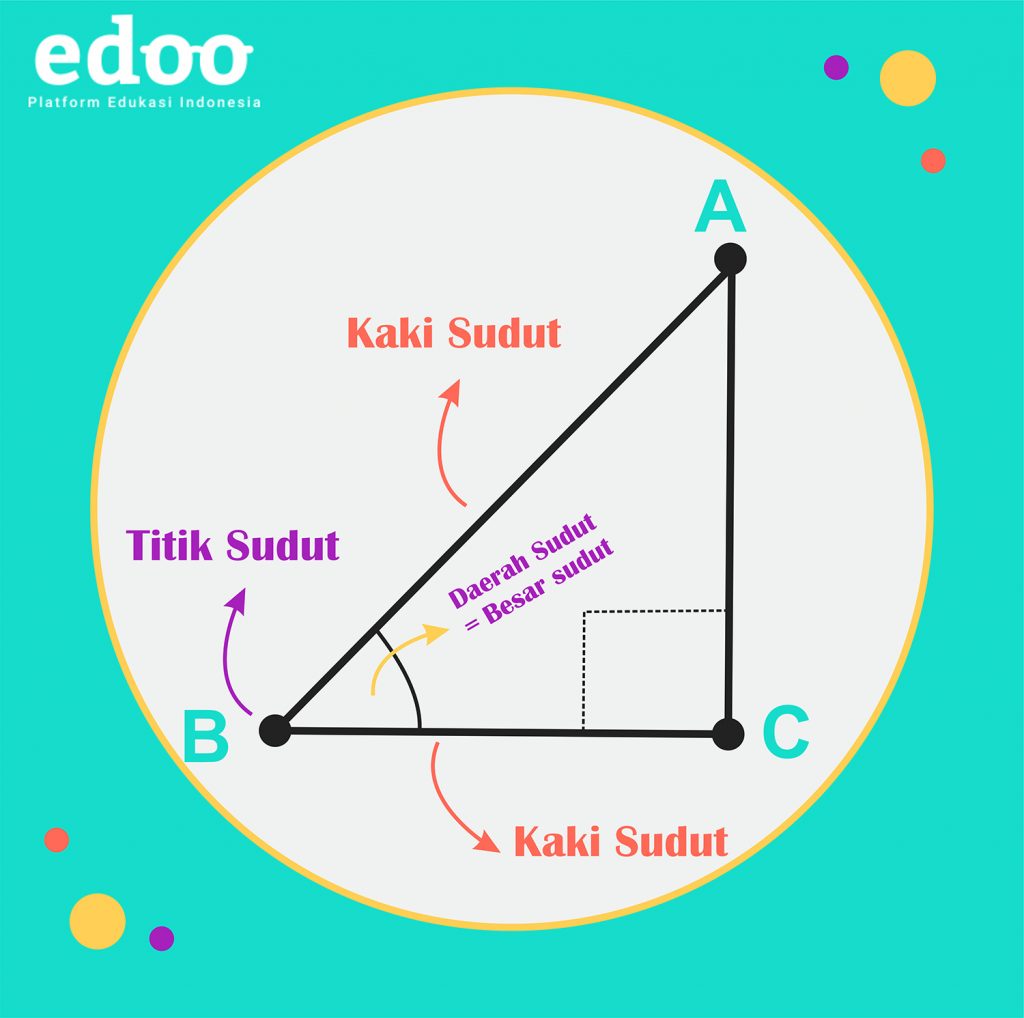
Secara umum, sudut didefinisikan sebagai daerah yang dibentuk oleh dua sinar garis (garis lurus yang berawal dari satu titik) yang saling berpotongan. Titik perpotongan tersebut disebut sebagai titik sudut, sedangkan kedua sinar garis disebut sebagai kaki sudut. Sudut dapat dilihat sebagai ruang antara dua garis yang saling bertemu. Dalam notasi matematika, sudut dilambangkan dengan simbol ∠, misalnya ∠ABC, yang berarti sudut yang terbentuk di titik B antara garis AB dan BC.

Besarnya sudut diukur menggunakan satuan derajat (°), dengan rentang dari 0° hingga 360°. Sudut 0° terjadi ketika dua garis berimpit secara sempurna, sedangkan sudut 360° merupakan sudut penuh yang melingkupi seluruh lingkaran. Dalam praktiknya, sudut sering digunakan untuk menggambarkan posisi, arah, dan hubungan antar objek dalam ruang. Contohnya, dalam navigasi, sudut digunakan untuk menentukan arah perjalanan, sementara dalam seni, sudut membantu menciptakan kesan dimensi dan perspektif.

Jenis-Jenis Sudut Berdasarkan Besarannya

Dalam matematika, sudut dibagi menjadi beberapa jenis berdasarkan besarnya. Berikut penjelasan mengenai masing-masing jenis sudut:

1. Sudut Lancip
   
   Sudut lancip adalah sudut yang besarnya kurang dari 90°. Bentuknya terlihat runcing dan tajam. Secara matematis, sudut lancip dinyatakan dengan 0° < x < 90°. Contoh sudut lancip bisa ditemukan pada ujung segitiga sama sisi atau sudut antara jarum jam dan menit pada pukul 02.00.

2. Sudut Siku-Siku
   
   Sudut siku-siku memiliki besar tepat 90°. Bentuknya mirip huruf L. Sudut ini sering ditemukan pada sudut bangunan, layar komputer, atau benda-benda persegi. Dalam notasi matematika, sudut siku-siku biasanya ditandai dengan tanda kotak kecil di sudutnya.

3. Sudut Tumpul
   
   Sudut tumpul adalah sudut yang besarnya lebih dari 90° tetapi kurang dari 180°. Bentuknya lebih lebar daripada sudut lancip dan siku-siku. Contohnya, sudut antara jarum jam dan menit pada pukul 04.00.

4. Sudut Lurus
   
   Sudut lurus memiliki besar tepat 180°, yang membuatnya terlihat seperti garis lurus. Sudut ini terbentuk ketika dua garis berpotongan secara langsung tanpa membentuk sudut tajam.

   Baca juga: Apa Itu Foto Copy? Pengertian dan Fungsi Pentingnya

5. Sudut Refleks
   
   Sudut refleks adalah sudut yang besarnya lebih dari 180° tetapi kurang dari 360°. Bentuknya melengkung dan lebih dari setengah lingkaran. Contoh sudut refleks bisa dilihat saat jam menunjukkan waktu tertentu yang melampaui 180°.

6. Sudut Penuh
   
   Sudut penuh memiliki besar tepat 360°, yang membentuk lingkaran utuh. Sudut ini terbentuk ketika dua garis berputar penuh mengelilingi satu titik.

7. Sudut Nol Derajat
   
   Sudut nol derajat terjadi ketika dua garis berimpit secara sempurna, sehingga tidak membentuk daerah sudut sama sekali.

Jenis-Jenis Sudut Berdasarkan Hubungannya

Selain dibedakan berdasarkan besarannya, sudut juga dapat dikategorikan berdasarkan hubungan antara dua sudut. Berikut penjelasan mengenai masing-masing jenis sudut ini:

1. Sudut Berpenyiku (Komplementer)
   
   Sudut berpenyiku adalah dua sudut yang jika dijumlahkan besarnya sama dengan sudut siku-siku, yaitu 90°. Contohnya, jika satu sudut besarnya 30°, maka sudut penyiku-nya adalah 60°.

   Baca juga: Cara menggambarkan sudut dengan akurat dalam seni lukis

2. Sudut Berpelurus (Suplementer)
   
   Sudut berpelurus adalah dua atau lebih sudut yang jika digabungkan besarnya tepat 180°, membentuk sudut lurus. Contohnya, sudut 120° dan 60° adalah sudut berpelurus.

3. Sudut Berdampingan
   
   Sudut berdampingan adalah sudut yang memiliki titik sudut yang sama dan salah satu kakinya berimpit. Kedua sudut ini saling berdekatan tetapi tidak saling tumpang tindih.

4. Sudut Bertolak Belakang
   
   Sudut bertolak belakang adalah sudut yang terbentuk dari dua garis yang saling berpotongan dan posisinya berlawanan, baik secara vertikal maupun horizontal. Contohnya, pada huruf X, sudut-sudut yang berlawanan disebut sudut bertolak belakang.

Penerapan Sudut dalam Kehidupan Sehari-Hari

Pemahaman tentang sudut tidak hanya berguna dalam matematika, tetapi juga dalam berbagai aspek kehidupan sehari-hari. Misalnya, dalam arsitektur, para arsitek menggunakan sudut untuk merancang bangunan yang stabil dan indah. Dalam olahraga, atlet sepak bola memperhatikan sudut tendangan agar bisa menciptakan peluang gol yang optimal. Dalam navigasi, kapten kapal atau pilot menggunakan sudut untuk menentukan arah perjalanan. Bahkan dalam seni, sudut digunakan untuk menciptakan efek visual yang menarik.

Di dunia teknologi, sudut juga menjadi faktor penting dalam desain layar smartphone, tablet, dan monitor. Misalnya, sudut pandang layar (viewing angle) memengaruhi kenyamanan pengguna saat melihat layar dari berbagai sudut. Dalam robotik, sudut digunakan untuk mengontrol gerakan dan posisi robot.

Tips untuk Mempelajari Sudut dengan Efektif

Untuk memahami sudut secara lebih mendalam, berikut beberapa tips yang bisa Anda coba:

• Gunakan alat bantu seperti busur derajat untuk mengukur dan menggambar sudut.
• Latih diri dengan mengerjakan soal-soal geometri yang berkaitan dengan sudut.
• Coba mengidentifikasi sudut-sudut di sekitar Anda, seperti sudut bangunan, meja, kursi, atau benda-benda lainnya.
• Pelajari hubungan antar sudut, seperti sudut berpenyiku, berpelurus, dan bertolak belakang.
• Jelaskan konsep sudut kepada orang lain untuk memperkuat pemahaman Anda.

Dengan memahami jenis-jenis sudut dan penerapannya, Anda tidak hanya akan lebih mudah dalam menyelesaikan soal matematika, tetapi juga akan lebih peka terhadap lingkungan sekitar. Sudut adalah bagian tak terpisahkan dari dunia kita, dan dengan memahami konsepnya, kita bisa lebih menghargai keindahan dan logika yang tersembunyi di balik bentuk-bentuk yang kita lihat setiap hari.