Pengertian dan contoh kelompok besaran turunan menjadi salah satu konsep penting dalam ilmu fisika. Dalam pembelajaran fisika, siswa seringkali dihadapkan pada berbagai jenis besaran yang dibagi menjadi dua kategori utama, yaitu besaran pokok dan besaran turunan. Besaran turunan merupakan hasil dari kombinasi beberapa besaran pokok, sehingga memiliki satuan dan dimensi yang diturunkan dari besaran pokok tersebut.
Besaran turunan memainkan peran krusial dalam berbagai bidang kehidupan, termasuk teknologi, rekayasa, dan sains modern. Contohnya, kecepatan yang merupakan turunan dari panjang dan waktu, atau gaya yang berasal dari massa dan percepatan. Pemahaman yang baik tentang besaran turunan sangat penting untuk memahami konsep-konsep fisika yang lebih kompleks.
Dalam artikel ini, kita akan membahas secara lengkap pengertian besaran turunan, bagaimana mereka terbentuk dari besaran pokok, serta contoh-contoh besaran turunan yang umum digunakan dalam ilmu fisika. Selain itu, kita juga akan melihat bagaimana besaran turunan digunakan dalam kehidupan sehari-hari dan penelitian ilmiah. Dengan demikian, artikel ini bertujuan untuk memberikan wawasan mendalam mengenai kelompok besaran turunan dalam konteks ilmu fisika.
Apa Itu Besaran Turunan?
Besaran turunan adalah jenis besaran yang diperoleh melalui kombinasi atau perhitungan dari beberapa besaran pokok. Berbeda dengan besaran pokok yang sudah ditetapkan secara internasional dan tidak dapat didefinisikan lagi, besaran turunan memiliki satuan dan dimensi yang berasal dari besaran pokok. Misalnya, luas merupakan turunan dari besaran panjang, sedangkan kecepatan merupakan gabungan dari besaran panjang dan waktu.
Kombinasi ini dilakukan melalui rumus-rumus tertentu, sehingga menghasilkan besaran baru yang memiliki makna fisis yang spesifik. Contohnya, energi adalah hasil dari perkalian antara gaya dan jarak tempuh, sehingga satuan energi (joule) berasal dari satuan gaya (newton) dan satuan panjang (meter).
Contoh Besaran Turunan dalam Ilmu Fisika
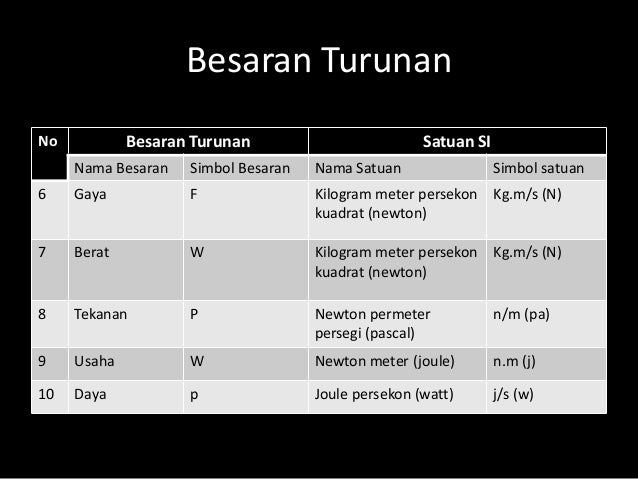
Beberapa contoh besaran turunan yang umum ditemukan dalam ilmu fisika antara lain:
- Luas: Diukur dalam meter persegi (m²), diperoleh dari perkalian panjang dan lebar.
- Volume: Diukur dalam meter kubik (m³), diperoleh dari perkalian panjang, lebar, dan tinggi.
- Kecepatan: Diukur dalam meter per detik (m/s), diperoleh dari pembagian perpindahan dengan waktu.
- Gaya: Diukur dalam newton (N), diperoleh dari perkalian massa dengan percepatan.
- Tekanan: Diukur dalam pascal (Pa), diperoleh dari pembagian gaya dengan luas permukaan.
- Usaha dan Energi: Diukur dalam joule (J), diperoleh dari perkalian gaya dengan jarak tempuh.
- Daya: Diukur dalam watt (W), diperoleh dari pembagian usaha dengan waktu.
- Percepatan: Diukur dalam meter per detik kuadrat (m/s²), diperoleh dari pembagian kecepatan dengan waktu.
- Frekuensi: Diukur dalam hertz (Hz), diperoleh dari jumlah getaran per detik.
- Momentum: Diukur dalam kilogram meter per detik (kg·m/s), diperoleh dari perkalian massa dengan kecepatan.
- Massa Jenis: Diukur dalam kilogram per meter kubik (kg/m³), diperoleh dari pembagian massa dengan volume.
- Muatan Listrik: Diukur dalam coulomb (C), diperoleh dari perkalian arus listrik dengan waktu.
- Beda Potensial Listrik: Diukur dalam volt (V), diperoleh dari pembagian energi dengan muatan listrik.
- Kapasitansi: Diukur dalam farad (F), diperoleh dari perkalian muatan listrik dengan beda potensial.
- Hambatan Listrik: Diukur dalam ohm (Ω), diperoleh dari pembagian tegangan listrik dengan arus listrik.
- Fluks Magnet: Diukur dalam weber (Wb), diperoleh dari perkalian induksi magnet dengan luas bidang.
- Panjang Gelombang: Diukur dalam meter (m), diperoleh dari perkalian cepat rambat gelombang dengan periode.
- Intensitas Cahaya: Diukur dalam candela (Cd), diperoleh dari pembagian fluks cahaya dengan sudut ruang.
- Kuat Medan Magnet: Diukur dalam tesla (T), diperoleh dari perkalian konstanta permeabilitas dengan arus listrik dibagi 2 kali jari-jari lingkaran.
- Rapat Arus: Diukur dalam ampere per meter persegi (A/m²), diperoleh dari perkalian luas arus dengan luas penampang kawat.
Peran Besaran Turunan dalam Kehidupan Sehari-Hari
Besaran turunan tidak hanya relevan dalam studi ilmu fisika, tetapi juga berperan penting dalam kehidupan sehari-hari. Contohnya, ketika kita mengukur kecepatan kendaraan, kita menggunakan satuan meter per detik (m/s). Atau saat menghitung daya alat elektronik, kita menggunakan satuan watt (W). Dengan pemahaman yang baik tentang besaran turunan, kita bisa lebih mudah memahami cara kerja berbagai alat dan fenomena alam.
Selain itu, besaran turunan juga digunakan dalam berbagai bidang seperti teknik, kedokteran, dan lingkungan. Misalnya, dalam bidang kedokteran, tekanan darah diukur dalam satuan mmHg (milimeter raksa), yang merupakan bentuk dari besaran tekanan. Dalam lingkungan, massa jenis air digunakan untuk menentukan apakah suatu benda akan tenggelam atau mengapung.
Pentingnya Pemahaman Besaran Turunan
Memahami besaran turunan sangat penting bagi para pelajar, peneliti, maupun masyarakat umum. Pemahaman ini membantu kita dalam menginterpretasi data, melakukan perhitungan, dan merancang alat atau sistem yang lebih efisien. Dalam pendidikan, besaran turunan menjadi dasar untuk memahami konsep-konsep yang lebih kompleks seperti hukum Newton, hukum Ohm, dan prinsip-prinsip termodinamika.
Selain itu, pemahaman tentang besaran turunan juga membantu dalam pengembangan teknologi. Misalnya, dalam pengembangan perangkat elektronik, pemahaman tentang kapasitansi dan hambatan listrik sangat penting agar perangkat dapat bekerja dengan optimal. Dalam bidang energi, pemahaman tentang daya dan energi membantu dalam merancang sistem tenaga yang lebih efisien dan ramah lingkungan.
Kesimpulan
Kelompok besaran turunan merupakan bagian penting dalam ilmu fisika yang tidak dapat dipisahkan dari berbagai konsep dan aplikasi nyata. Dengan memahami besaran turunan, kita tidak hanya mampu menjelaskan fenomena alam, tetapi juga mampu merancang dan mengembangkan teknologi yang lebih baik. Melalui contoh-contoh yang telah disebutkan, kita dapat melihat betapa luas dan beragamnya penggunaan besaran turunan dalam kehidupan sehari-hari.
Dengan demikian, pemahaman yang mendalam tentang besaran turunan tidak hanya bermanfaat dalam studi ilmu fisika, tetapi juga sangat berguna dalam berbagai bidang kehidupan. Oleh karena itu, penting bagi setiap individu untuk mempelajari dan memahami konsep-konsep ini agar dapat memanfaatkannya secara optimal.














Komentar